LC Oscillations

In an LC oscillating circuit with $L=75 \mathrm{mH}$ and $C=30 \mathrm{\mu F}$, the maximum charge of capacitor is $2.7\times {10}^{-4} \mathrm{C}$. Maximum current through the circuit will be

In the circuit shown in figure $S_1$ is open and, $S_2$ and $S_3$ are closed. The circuit is in steady state. At time $t=0$, switch $S_1$, is closed and $S_2$ and $S_3$ are opened simultaneously. $V=100 \mathrm{V}$, $R=10 \mathrm{\Omega }, C=100 \mathrm{\mu F}, L=0.03 \mathrm{H}$

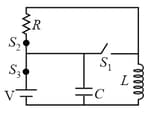
Find the maximum charge that will appear on the capacitor at any time

A capacitor of capacitance $0.6 \mu \mathrm{F}$ is charged by a $6 \mathrm{V}$ battery. Charged capacitor is now connected to an inductor of inductance $2 \mathrm{mH}$. Then find the current in the circuit when one third energy stored in capacitor converts into the energy stored in inductor.

In L.C oscillation, maximum current in the inductor can be $I$. If at any instant, electric energy and magnetic energy associated with circuit is equal, then current in the inductor at that instant is

In an L-C oscillation maximum charge on capacitor can be $Q_0$. If at any instant electrical energy is $\frac{3}{4}$th of the magnetic energy then the charge on capacitor at that instant is

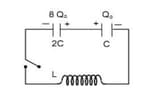
Two capacitors of capacitance $2\mathrm{C}$ and $C$ are given charges $8{\mathrm{Q}}_0$ and $Q_0$ respectively as shown in figure. If switch is closed what will be maximum current through inductor.

In an $L-C$ circuit shown in the figure, $C=1\mathrm{F}, L=4\mathrm{H}.$ At time $t=0,$ charge in the capacitor is $4 \mathrm{C}$ and it is decreasing at a rate of $\sqrt{5}\mathrm{C} {\mathrm{s}}^{-1}.$ Choose the correct statements.

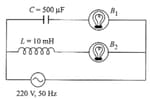
In the circuit shown in figure, if both the bulbs $B_1$ and $B_2$ are identical, then

A radio receiver can tune over the frequency range $300\mathrm{kHz}$ to $1200\mathrm{kHz}$. If the tunable $L C$ circuit has a fixed inductor$L=200\mu H$, what must be the range over which the capacitor must be tuned? (You can use${\mathrm{\pi }}^2\approx 10$ )

We connect a charge capacitor to an inductor the electric current and charge on the capacitor in the circuit undergoes LC oscillations.

What is the working of LC oscillator?

An $\mathrm{LC}$ resonant circuit contains a $400 pF$ capacitor and an inductor of $400 \mu \mathrm{H}.$ It is coupled to an antenna. Wavelength of radiated electromagnetic wave is

What is LC oscillation?

A $60\mu \mathrm{F}$ capacitor is charged to $100 \mathrm{volts}$. This charged capacitor is connected across a $1.5\mathrm{mH}$ coil, so that $\mathrm{LC}$ oscillations occur. The maximum current in the coil is:-

In an $LC$ circuit shown in figure, $C=2 \mathrm{F}$ and $L=2 \mathrm{H}$. At time $t=0$, charge on the capacitor is $3$ coulomb and it is decreasing with rate of $\sqrt{4} \mathrm{C} {\mathrm{s}}^{-1}$. Then choose the correct statement.

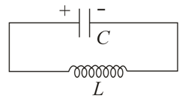
The natural frequency of the circuit is (in $\mathrm{rad} {\mathrm{s}}^{-1}$),

In an LC oscillator circuit L = 10 mH, C = 40µF. If initially at t = 0 the capacitor is fully charged with 4µC then find the current in the circuit when the capacitor and inductor share equal energies. 

The diagram shows a capacitor C and a resistor R connected in series to an AC source, V₁ and V₂ are voltmeters and A is an ammeter. Consider now the following statements :

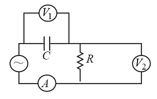
(I) Readings in A and V₁ are always in phase

(II) Readings in A and V₂ are always in phase

(III) Reading in V₁ is ahead with reading in V₂

Which of these statements are is correct : 

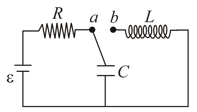
The switch in the circuit pictured is in position a for a long time. At t = 0 the switch is moved from a to b. The current through the inductor will reach its first maximum after moving the switch in a time : -

A LC circuit is in the state of resonance. if C = 0.1 µF and L = 0.25 henry. Neglecting ohmic resistance of circuit what is the frequency of oscillations :